Okay, here’s how I would do it if I were forced to use the simplest Automator elements. Honestly, doing this in a scripting language (which Automator could run) tends to be quicker and less fiddly, but probably would make little if any sense at all if you were just starting out.
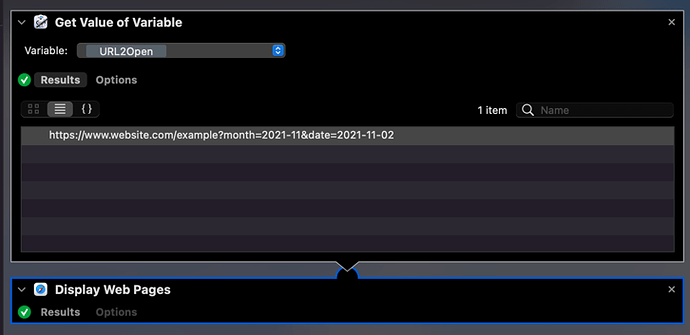
So here’s the workflow. Two steps. One get’s a variable, the other opens the value retrieved from the variable. As you might guess from the steps and name, the variable contains the URL to open.
All the set-up of the variable is defined outside the “flow” part of the workflow. An aspect I always found counter intuitive, but that may just be me.
I created three variables to try and help explain this.
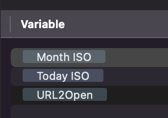
If I edit URL2Open, you can see it consists of the URL (size means you can only see some of it), plus the other two variables you saw above.
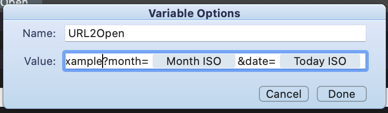
I dragged these in from the list above when I needed to use them.
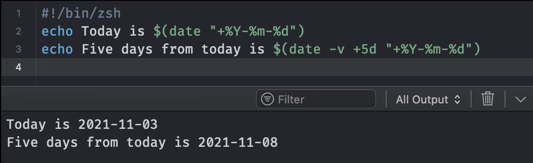
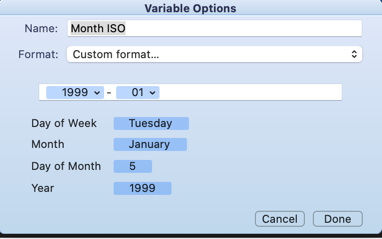
They just define the two sets of date data in the formats you specified.
Month ISO
Today ISO
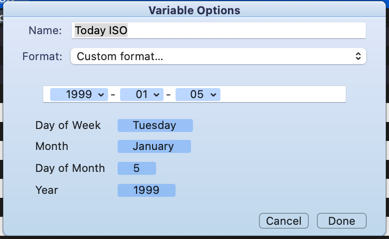
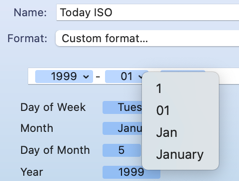
To create these, you type in the hyphens and you drag the component parts in the window into the field. But, you may notice that the month is a word, yet I have a number in the field. Note the little drop down marker on the right of the month token in the value field. If you click on it to expand it, you get to choose a different format.
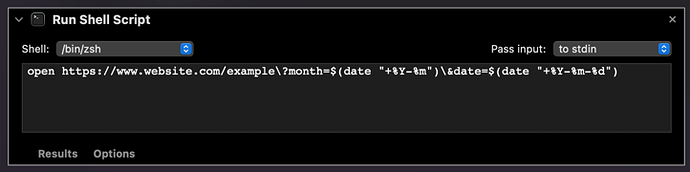
For completeness, here’s a workflow that does the same thing using a single script line. It works in just the same sort of way, and now I’ve been through the workflow above, it might give you a bit of insight to what this is doing. The algorithm is practically identical. The script is a lot faster to create and edit (Shortcuts is great, but Automator’s dragging of variable tokens I find incredibly painful in comparison), but your starting point is effectively the proverbial blank page, and you have to know how to get there, whereas Automator’s prebuilt actions are giving you everything all in.
If you are running, or planning to move to Monterey (the new version of macOS), the Shortcuts app is available on that OS, and is intended to be Automator’s successor on the Mac. That would be worth you exploring. It’s a more recent creation, but builds strongly on Automator’s approach. It has received a lot more attention than Automator and as a result, I suspect most people find it easier to use. Certainly building this workflow would be almost as fast as writing a line of script … though like Automator, you could even run script from it.
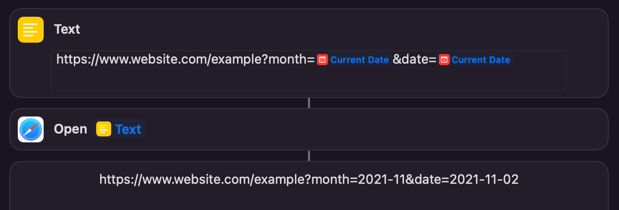
Here the use of current date (a standard variable) get’s the same formatting effect as in the above options. It opens the page, and you can see the URL that was passed through shown after the Open URLs action. You could put the content of the text action into the Open URL step to make it a one step shortcut … except when I tried that it failed (though it worked on iOS and iPadOS) - it is still very new on the Mac and there are still some rough edges.
I hope the above helps.